In this three-part series, I want to share some of the work I did for fun during the 2018 AFL season. In particular, this work is about using a Bayesian model to estimate AFL team ratings. In Part 1, I give a brief introduction to a rating system known as Elo. In Part 2, I will share how a Bayesian approach can be used to estimate the parameters of the Elo system. I will also share some results on how the model tracked the changes in team ratings as the 2018 AFL season progressed. One of the advantages of using a Bayesian Elo framework is that it allows us to capture the uncertainty or the randomness in team ratings. Incorporating this uncertainty in the ratings is crucial for avoiding over confident win/lose predictions for matches. What exactly I mean by this would become clearer in Part 2. In Part 3, I will show how we can use simulations to estimate the probabilities of the tournament outcome (of course, before the tournament ends). The source code for this work can be found here.
What is Elo?
Elo system, named after the inventor Arpad Elo, was developed originally to rank Chess players. However, Elo has been extended to other sports including soccer, basketball, tennis, etc.
At the heart of the system is a formula to update the ratings of two teams after the outcome of a match between them is available. The change in the teams’ ratings are based on:
- the current ratings of the two teams,
- the outcome of the match (win/lose/tie) or the scores against each other,
- the Elo parameters $K$ and $\tau$.
How does it work?
Assume that two teams $i$ and $j$ have current Elo ratings of $r_{i,\text{old}}$ and $r_{j,\text{old}}$, respectively. Define the difference between the current Elo ratings, $\delta_{i,j}$, as
\begin{equation} \delta_{i,j} = r_{i,\text{old}} - r_{j,\text{old}}. \end{equation}
Once the outcome, $S_{i,j}$, of a match between the two teams is observed, the Elo ratings for each team are updated to $r_{i,\text{new}}$ and $r_{j,\text{new}}$ according to
where
and
Here $K$ and $\tau$ are parameters of the Elo system known as “K-factor” and “logistic parameter”, respectively. Conventionally, the values of $K$ and $\tau$ are set by the ranking authority/modeller. For example, in International Chess Federation’s current Elo implementation, parameters are set as $K = 40$ and $\tau = 400$ for a new player until he/she has completed events with at least 30 games.
Let’s work through an example. Assume that two teams A and B with current Elo ratings of 1300 and 1600 played a match against each other and team B won. For an Elo system with $K = 40$ and $\tau = 400$, the updated rankings for each team are as follows;
Next let’s focus on some properties of Elo.
Not all wins and losses are treated equal
What I mean by this is, a win of a highly-rated team against a very poorly rated team barely changes the ratings, while losing to such a team penalise the ratings of the top team disproportionately. Consider the following example, which is a continuation of the last example. Assume that team A’s current Elo rating is 500 (instead of 1300). When compared against an initial Elo score of 1600 for team B, A’s rating is significantly lower. If team B wins against team A, the Elo score of team B would increase just marginally from 1600 to 1600.071. On the other hand, if team B lost to team A, the Elo rating of team B would incur a substantial drop to a new rating of 1560.071. Similarly, losing to a very strong team alter the Elo rating of the weak team just marginally, whereas a win against a strong team results in a disproportionate gain in the rating.
Conservation of average Elo
This is also known as the zero-sum rule and means that if $S_{A,B} + S_{B,A} = 1$ then an increase in team A’s Elo is equal to the decrease in team B’s Elo and vice versa. In other words,
\begin{equation} r_{A,\text{new}} - r_{A,\text{old}} = r_{B,\text{old}} - r_{B,\text{new}}. \end{equation}
This implies that the average Elo value across all the teams remain constant despite fluctuations in individual team ratings.
K factor
K value directly affects the volatility of the ratings. A larger K values means that even a marginally better performance from a team, changes its rating by a significant amount. On the other hand, a very small value of K, causes just a little shift in the team’s rating despite an exceptional performance. The ratings remain static indefinitely in the extreme case of $K = 0$.
logistic parameter $\tau$
How does a difference in Elo ratings between A and B translate into likelihood of team B winning compared to that of team A? Logistic parameter can help answer this and put some context in to the Elo difference. Recall that $\mu_{A,B}$ is a number between 0 and 1. This could be treated as the expected probability of team A winning against team B. With some algebra, it can be shown that \begin{equation} \frac{\mu_{A,B}}{\mu_{B,A}}= 10^{(r_{A,\text{old}}-r_{B,\text{old}})/\tau} . \end{equation}.
Notice that an Elo difference of $\tau$ means the probability that team A wins against team B is 10 times more than the probability of team B beating team A. More generally, the odds of team A winning increases tenfold for each increment of $\tau$ in the difference of Elo ratings.
Accounting for margin of victory
The $S_{i,j}$ parameter defined earlier does not differentiate between a win by a mere point and a win by a significant point margin. This clearly is not desirable. Let $h_{i,j}$ denote the score that team $i$ scored against team $j$. A simple modification to take the margin of victory into the Elo system is to incorporate the team scores by redefining $S_{i,j}$ as \begin{equation} S_{i,j} = \frac{h_{i,j}+1}{h_{j,i} + h_{i,j} + 2}. \end{equation}
Note that even after this modification \begin{equation} S_{i,j} + S_{j,i} = 1. \end{equation}
Limitations
In the vanilla Elo system considered here, important factors such as player substitution, injuries, team dynamics, and home field advantage are not taken into account. These factors could have a material influence towards the outcome of a game. Although, home field advantage can be somewhat accounted for by some modifications, for the purposes of the current exercise, I have kept it simple and proceeded with the vanilla Elo system.
For further information on Elo or ranking and rating in general, I recommend the book Who’s #1?: The Science of Rating and Ranking by Amy N. Langville.
Bayesian Elo?
Rather than assuming the parameters $K$ and $\tau$ as fixed parameters, what if I treat them as random parameters and use data (match outcomes) to estimate them? This means that team ratings in turn, become random quantities. Intuition suggests that it would be a better approach for modelling as it allows to capture the uncertainty of these parameters. I used Stan to implement my version of the Bayesian Elo for AFL. To give a sneak peek of what this approach enables, I present below, posterior probability density functions of some the the parameters that were estimated.

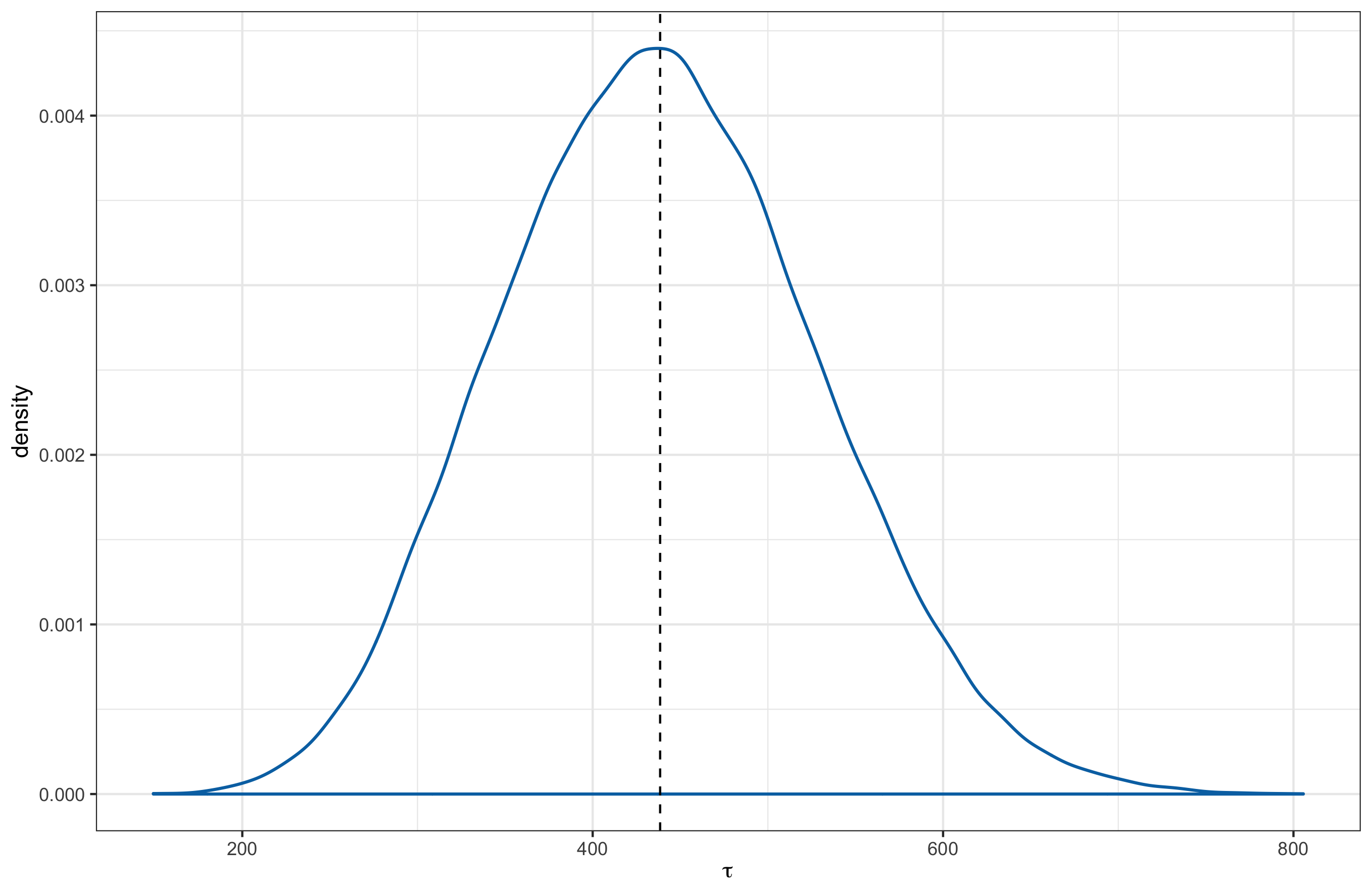

Next, in Part 2, I go in to more details on the Bayesian Elo model.
